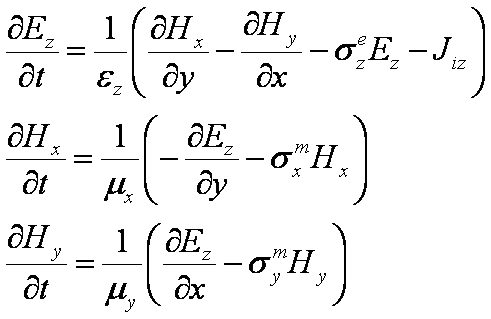
I have found the Finite Diference Time Domain

I have found the Finite Diference Time Domain (FDTD)

method could be suitable to solve my problem - this equations - 2D analyses:

z-direction is infimity. I need a relative permeability set higher then 1

on the part of 2D model. I would like to use the Meep. Is it suitable?

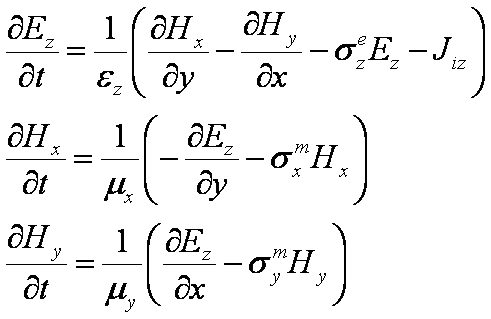
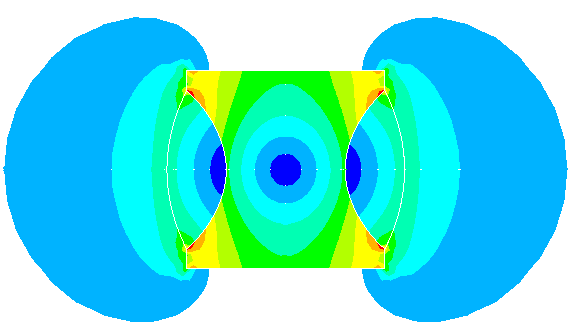
In the next I need to do my test analysis is to have initial 2D magnetic field which is get from

quasi static analysis with optimally fast driven sinus function current.

There is initial 2D magnetic field figure here:

After that to run transient FDTD analysis. The electromagnetic waves should be excited. Maybe

some small initial electric field should be inputed (as imperfection in z-direction)

MAGNETIC FIELD SHOULD BE COLAPSING OSCILATING WITH CORE NATURAL FREQUENCE.

I have tried to solve this transient problem with implicit solver as harmonic analyses given

by Fourier series. This way is difficult.

THE COMPUTING MODEL SHOULD INCLUDE EARTH ELECTROSTATIC CHARGE INSTENSITY

E=66-120 [Vm^-1]

THEN IT STARTS TO HAVE PHYSICAL MEANING.

I do not plan nonlinear material models, I would like to have a part of the 2D model (core)

with relative permeability around 100 and resistivity (to not to be overdamped) as engine core.

To do energy transfer not to mechanical work, but to core heat to simplify problem.

Boundary condition should be impedance and I would like to evaluate Poynting vectors on the boundary.

THIS SHOULD BE FREE ENERGY DEVICE WHICH TAKES ELECTRICITY FROM SPACE!!!

I WOULD BE VERY GLAD IF MY THEORY IS TESTED.